Аналитическая реология. Определение молекулярного веса и ММР полимеров.
Аналитическая реология занимается определением микроструктуры материала на основе измерений вязкоупругих свойств. Аналитическая реология является разделом аналитической химии в области свойств течения. Аналитическая реология может быть применена для исследования различных материалов, в которых реологические свойства связаны с микроструктурой. Существует много таких применений. Например, по линейности вязкоупругого поведения можно определить распределение размера частиц в мультифазной суспензии. Экспериментальные методы определения линейных вязкоупругих свойств материалов хорошо развиты из-за точности и воспроизводимости измерений, которые могут быть выполнены рутинным высокоавтоматизированным способом. Аналитическая реология использует эту экспериментальную возможность и предлагает расширенные методы интерпретации и применения стандартных реологических измерений. Обладая расширенными методами обработки данных, например определение ММР, программа TAOrchestrator позволяет реализовать все возможности реологии. В этой статье мы рассмотри специфическое применение аналитической реологии для расчета молекулярно-массового распределения линейных нежестких полимеров по результатам измерения вязкоупругих свойств материалов.
В настоящее время существует множество убедительных методов для определения молекулярно-массового распределения гибкоцепных полимеров, такие как, гельпроникающая хроматография, рассеяние света, определение характеристической вязкости и т.д., поэтому важно знать какие преимущества имеет реологический способ определения ММР. Существует ряд преимуществ реологических методов определения молекулярно-массового распределения. Например, практически все традиционные методы определения ММР предполагают растворимость полимера в растворителях при комнатной температуре. Однако многие важные полимеры, такие как политетрафторэтилен, полиэтилен и полипропилен в таких условиях растворяются только частично. Это несколько затрудняет определение традиционными методами ММР этих полимеров. Реологические методы не требуют длительной процедуры растворения. На самом деле получение реологических данных для расплава полиэтилена или полипропилена не представляет каких-либо экспериментальных трудностей. Надо отметить, что такие реологические методы требуют калибровочных образцов, аттестованных независимым методом. Даже если традиционные методы могли бы быть использованы, их чувствительность и селективность недостаточны, особенно для высокомолекулярного «хвоста». С практической точки зрения, определение вклада высокомолекулярной части очень важно для установления свойств полимеров. Реологические методы определения ММР существенно чувствительней к высокомолекулярному концу молекулярно-массового распределения. Это легко понять из рассмотрения прямой зависимости линейно-вязкоупругих свойств материалов от молекулярной массы и молекулярно-массового распределения. Для примера, хорошо известно, что вязкость при нулевой скорости сдвига пропорциональна молекулярному весу в степени 3,4. Таким образом при небольшом вкладе в среднюю молекулярную массу оказывается сильное влияние на вязкость при нулевой скорости сдвига и, соответственно, повышает чувствительность метода. Однако только часть линейно-вязкоупругого спектра содержит информацию о молекулярной массе системы. Это явление описывается так называемой теоремой Bueche-Ferry /1/. В частности, в соответствии с гипотезой Bueche-Ferry в достаточно коротких масштабах времени поведение гибкоцепных полимеров схоже, независимо от молекулярной массы, характера цепи и концентрации полимера.
Это предполагает, что ММР не влияет на вязкоупругие свойства в стеклообразном состоянии. Физически, это основано на том факте, что эффект клубка возникает при значительно больших длинах в сравнении с размером мономера.
Следовательно, все зависимости механических свойств от молекулярного веса полностью исчезают в частотно-временном диапазоне, характерном для стеклообразного состояния. Рис. 1 иллюстрирует различные режимы динамического отклика для расплава монодисперсного полимера. Не смотря на ограничения частотно-временного диапазона, в котором должны быть собраны данные с точки зрения практики, наличие «застеклованного поведения" требуется, как эффективное средство устранения этих эффектов из экспериментальных данных до расчета ММР.>
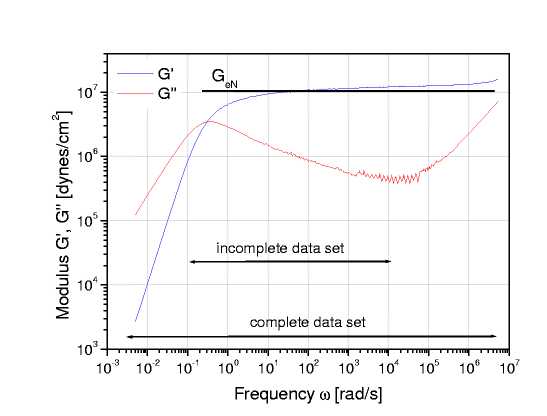
Рисунок 1: Реологические кривые для монодисперсного линейного гибкоцепного полимера.
Основная сложность в том, что модель Рауза для высокомолекулярных компонентов может комбинироваться с рептационной моделью для низкомолекулярной части. Ниже описан метод, используемый нами для учета этого эффекта.
ПРАВИЛА СМЕШЕНИЯ ДЛЯ РАСПЛАВОВ ПОЛИМЕРОВ
Количественную связь между наблюдаемыми механическими свойствами полидисперсных расплавов и микроструктурой называют правилом смешения (mixing rule). Мы будем касаться правила смешения исключительно для линейных вязкоупругих свойств гибкоцепных полимеров. Правило смешения для гомогенных систем полимеров независимо было сформулировано Tsenoglou и des Cloizeaux /2,3/. Правило смешения названо "двойной рептационной" моделью и это относительно простая математическая аппроксимация более строгой и сложной молекулярной теории полидисперсности. Двойное рептационной правило смешения имеет следующее математическое выражение:
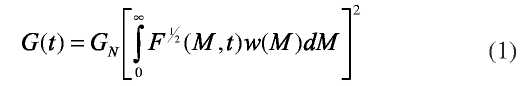
Где G(t) – модуль релаксации, который может быть определен из некоторых комбинаций экспериментов определения линейной вякоупругости, обсуждаемых ниже. F1/2(M,t) - функция монодисперсной релаксации, которая описывает временную релаксацию нагрузки монодисперсного полимера в ответ на малое смещение. w(M) – молекулярно-массовое распределение. Физически, все компоненты молекулярно-массового распределения в некоторой степени будут иметь вклад в модуль. Это идея зафиксирована в интеграле молекулярно-массового распределения w(M), который суммирует вклады всех компонентов ММР в G(t) с учетом функции F1/2 (M,t). Величина вклада каждого компонента будет зависеть от взаимодействия с другими молекулами. Это характеристика эффекта «смешения», которое описывается, как один компонент сложного молекулярно-массового распределения, при этом динамически взаимодействует со всеми соседями.
Программное обеспечение TAOrchestrator также имеет возможность работать с, так называемым, «средневзвешенным» правилом смешения, предложенным Marin и др./4/
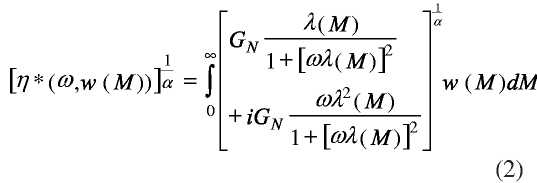
Средневзвешенное правило смешения (2) является полностью эмпирическим. Физическая база этого правила смешения основана на зависимости изменения размера от молекулярной массы в степени ~3,4. Для расчета молекулярно-массового распределения конкретного материала используя (1) необходимо иметь исходные данные для расчета с помощью программного обеспечения. Особенно важно знать значение модуля на горизонтальном участке GN и описание функции монодисперсной релаксации F1/2(M,t). Значение модуля GN присутствует в ряде справочников. Представление функции монодисперсной релаксации может иметь несколько вариантов. В основном мы будем использовать экспоненциальную форму,
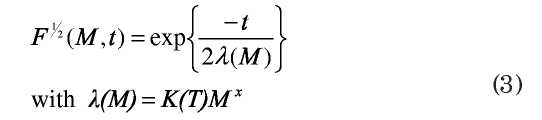
Где λ(M) характеристическое время релаксации для монодисперсной системы и K(T) – коэффициент, зависящий от температуры. Экспонента χ обычно имеет величину ~3.4 для гибкоцепных полимеров. Возможны другие варианты для функции монодисперсной релаксации, например, Doi-Edwards.
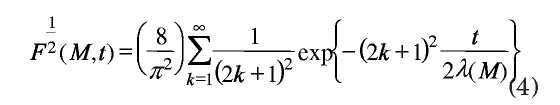
В общем случае, точность экспериментальных данных недостаточна для значительного различия в ММР, полученному по уравнению (1) с учетом (3) или (4). Температурная зависимость K(T) моделируется по аналогии с энергией активацией Аррениуса, хотя возможны варианты, например на основе уравнения Вильямса-Ланделла-Ферри. Величины параметров могут быть получены из литературных данных. Для новых полимеров, скорее всего, потребуется калибровка.
РАСЧЕТ МОДУЛЯ РЕКЛАКСАЦИИ ИЗ ДАННЫХ ЛИНЕЙНОЙ ВЯЗКОУПРУГОСТИ /5/
Существует значительное число методов для определения модуля релаксации G(t) на основе данных линейной вязкоупругости. Однако на практике, конкретные методы более или менее чувствительны к различным временным масштабам. Для примера, эксперимент с восстановлением вынужденной эластичности чувствителен к долговременным процессам, в то время как измерение динамического модуля - к быстротекущим релаксационным процессам. ПО TAOrchestrator предоставляет эффективные средства для комбинирования таких данных, что позволяет расширить диапазон определяемого модуля релаксации. Как правило, всегда полезно использовать данные линейной вязкоупругости из большего числа различных экспериментов для самосогласованного определения модуля релаксации во всем динамическом диапазоне, если конечно это возможно.
Как отмечалось ранее, только линейные вязкоупругие данные - пограничные и горизонтальные участки зависимости содержат информацию о молекулярном весе и молекулярно-массовом распределении. Поэтому, как только модуль релаксации рассчитан, кратковременные вклады стеклования должны быть устранены.
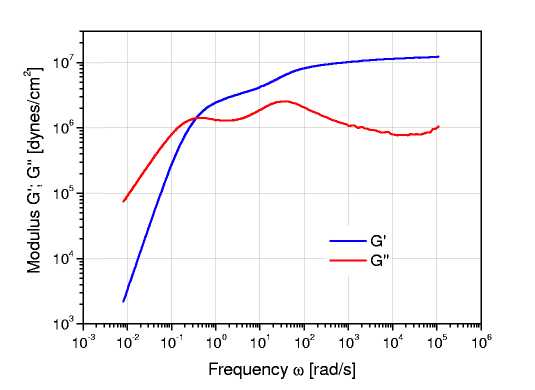
Рисунок 2: Зависимость для бидисперсной системы
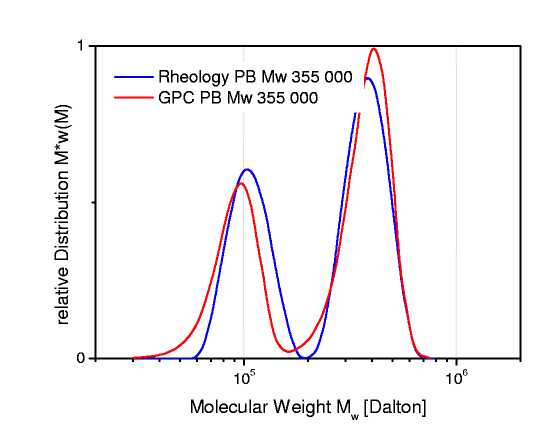
Figure 3: Значение ММР, полученное для бидисперсной смеси полибутадиена
ПО TA Orchestrator выполняет это при первой грубой оценке ММР. На основе оценки ММР определяется вклад модели Рауза, определенной как сумма вкладов для всех компонентов ММР. Затем эта величина вычитается из G(t). При экспериментальном определении модуля релаксации для расчета молекулярно-массового распределения существуют две различные экспериментальные возможности: 1) полный диапазон данных динамических модулей, 2) неполные данные динамических модулей. Данные считаются «полными» если они охватывают динамический диапазон время/частота от полностью терминального поведения до перехода в стеклообразное состояние (рисунок 1). Полные данные, обычно, могут быть получены при проведении исследовательских работ. На практике же, при рутинном анализе коммерческих продуктов с широким молекулярно-массовым распределением, чаще всего приходится иметь дело с «неполным» набором данных. В этом случае полностью терминальное поведение полимеров не достигается из-за исключительно длительных времен релаксации высокомолекулярной части или высокочастотный режим не доступен из-за инерционных ограничений реометра. Каждый из этих случаев представляет различный подход вычисления, результаты которого с ограничениями метода описаны далее.
ПОЛНЫЙ НАБОР ДАННЫХ ДИНАМИЧЕСКИХ МОДУЛЕЙ
Когда имеются величины динамических модулей от терминальной области до линейного участка, доступна вся реологическая информация, требуемая для преобразования в соответствии с правилом смешения. В этом случае проблема сводится к численному решению инвертированной двойной рептационной модели для ММР в стабильном и устойчивом виде. Двойное рептационное правило это интеграл Фредхольма (Fredholm) первого рода от W(M). Методы решения таких некорректно поставленных задач хорошо описаны. Молекулярно-массовое распределение рассчитывается с использованием дополняющих методов. Эти дополняющие методы доопределения применяются к моментам ММР, рассчитанным из экспериментальных данных с использованием преобразования Меллина (Mellin transforms) /5/. В результате получается надежный и робастный численный метод.
НЕПОЛНЫЙ НАБОР ДАННЫХ ДИНАМИЧЕСКИХ МОДУЛЕЙ
Когда экспериментальные данные не охватывают весь диапазон частот от граничной области до линейной набор данных считается неполным и к нему не может быть применена двойная рептационная модель без дополнительной информации.
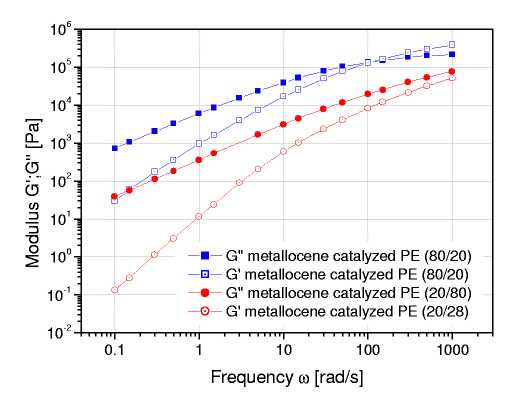
Рисунок 4: Реологические кривые бинарной смеси полиэтиленов
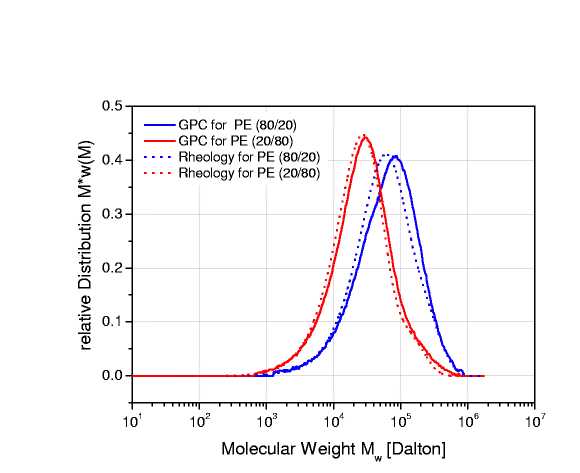
Рисунок 5: Рассчитанные ММР бинарных смесей полиэтиленов
ПО TAOrchestrator позволяет выполнять автоматический подбор, либо в ручном режиме. Эта возможность позволяет пользователю корректировать результаты и получать точные описания к конкретному диапазону данных. В ПО TAOrchestrator включено две модели молекулярно-массового распределения. Первая модель Весслау или нормальное логарифмическое молекулярно-массовое распределение, которое типично для продуктов полиприсоединения или полимеров, полученных на катализаторах Циглера-Натта. Вторая – распределение Шульца, которое обобщает наиболее вероятное молекулярно-массовое распределение более типичное для полимеров, получаемых поликонденсацией или полимеризацией на металлоценовых катализаторах.
ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ
На рисунках 2 и 3 представлены динамические модули и рассчитанные МР для бидисперсной системы полибутадиена. Для расчета ММР использовались полные наборы реологических данных. На рисунке 3 показаны ММР, полученные на основе реологического анализа, в сравнении с результатами ГПХ. Совпадение результатов реологии и ГПХ очень хорошее.
На рисунке 4 представлены две бинарные смеси полиэтилена, полученного на металлоценовых катализаторах. Для получения ММР были использованы неполные наборы данных динамических модулей. Для расчета использовался метод с комбинацией двух моделей Шульца молекулярно-массового распределения (рисунок 5). Точное совпадение результатов реологического анализа и ГПХ хорошо иллюстрируют применимость метода для анализа реальных коммерческих полимерных систем.
ССЫЛКИ
/l/ Doi,M.:JNNFM 23,151 (1987)
/2/ Tsenoglou,C.:ACS Polymer Preprints 28,185 (1987)
/3/ des Cloizeau, J.:Macromolecules 23, 4678 (1990)
/4/ Montfort.J.P. ;Marin,G.; Monge,P.: Macromolecules 17,1551 (1989)
/5/ Mead,D. J.Rheol. 38,1797 (1994)
